Pitágoras, matemático, filósofo, profeta nasceu na ilha de Samos, na Grécia, no século VI a.C. Existem muitos pontos obscuros sobre a sua história, mas, segundo alguns relatam, ele teria viajado pelo Egito e Babilônia, período durante o qual assimilou informações sobre Matemática e Astronomia, juntamente com várias ideias religiosas. Após retornar à Grécia fundou a Escola Pitagórica.
É atribuída a ele a elaboração da primeira demonstração geral de uma propriedade muito especial presente num tipo de triângulos também especial – o triângulo retângulo, que contém um ângulo de 90º. “O quadrado da hipotenusa é igual à soma dos quadrados das medidas dos catetos”, tanto é que hoje tal propriedade é conhecida como “Teorema de Pitágoras” que foi a inspiração da idéia de criar uma lixeira.
Mas existem documentos históricos demonstrando que casos particulares desse teorema já eram do conhecimento dos egípcios e babilônios muito antes dos gregos.
O momento não é de aprofundamento das diversas possibilidades do Teorema de Pitágoras, e sim, de passar uma compreensão do seu conceito básico, de modo a aplicá-lo também em situações mais complexas.
Em um triângulo retângulo, o quadrado construído sobre a hipotenusa é igual à soma dos quadrados construídos sobre cada um dos catetos.
A maneira tradicional de apresentar este Teorema é sob uma ótica algébrica. Neste pequeno estudo tentaremos, para facilitar a compreensão, apresentar também uma demonstração baseada no conceito de áreas.
Então, podemos representar este teorema com a seguinte expressão algébrica:
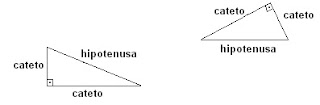
Vejamos uma representação gráfica, com os respectivos nomes de cada lado de um triângulo retângulo:
Como vemos nas figuras acima, Catetos são os dois lados (lados menores do triângulo) que forma um ângulo de 90º, enquanto a Hipotenusa (lado maior) é o lado oposto a esse mesmo ângulo, e que liga as duas extremidades dos catetos.
Mas vejamos um exemplo usando áreas, para facilitar ainda mais:
O triângulo retângulo a baixo é formado pela hipotenusa (a) que mede 10 cm, um cateto (b) que mede 6 cm e um cateto (c) que mede 8 cm.
Logo a baixo, fizemos uma área quadrada de cada um dos lados do triângulo. Ao formarmos um quadrado (quatro lados iguais), e subdividi-lo em quadrados com 1 cm, teremos então as seguintes áreas:
Hipotenusa(a): 5 x 5 = 25
Cateto (b): 3 x 3 = 9
Então podemos perceber que, ao somamos o resultado do quadrado do cateto b, 9, com o resultado do cateto c, 16, encontramos 25, que é exatamente igual ao quadrado da hipotenusa.
Tal equação pode ser representada por:
52 = 32 + 42, ou seja, 25 = 9 + 16.